Indice
L’analisi dei circuiti elettrici spesso è resa più semplice se una parte di circuito viene sostituita con un’altra equivalente; tale cioè che a seguito di tale sostituzione le correnti e le tensioni nella rimanente parte del circuito non subiscano variazioni
Equivalenza di reti attive e passive
Due reti (fig. E2-1a) una attiva, costituita da resistenze e da generatori ideali di tensione e/o di corrente comunque connessi, e l’altra passiva costituita solo da resistenze comunque connesse, possono essere sostituite con due circuiti equivalenti rispettivamente uno attivo e l’altro passivo (fig. E2-1b), tali che i valori di tensione e di corrente nel collegamento esterno non cambino.
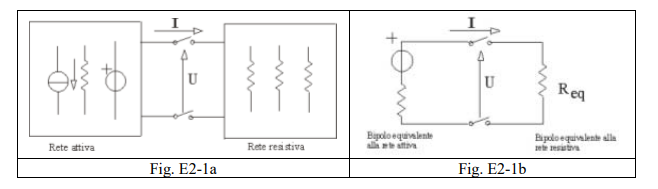
Il circuito equivalente della rete attiva (fig. E2-2) è costituito da un generatore di tensione (generatore di Thevenin) o da un generatore di corrente (generatore di Norton) . Il circuito equivalente della rete passiva è costituito da un bipolo resistivo.
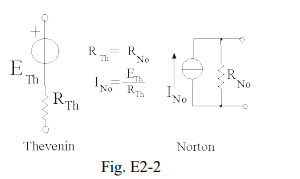
La determinazione del valore della resistenza di tale bipolo si ottiene in genere individuando eventuali bipoli connessi in serie e/o in parallelo e sostituendoli con idonei bipoli equivalenti; tale operazione viene ripetuta più volte fino ad ottenere un solo bipolo di tutta la parte di rete passiva di interesse. Più bipoli si dicono connessi in serie quando sono percorsi dalla stessa corrente, in parallelo quando sono sottoposti alla medesima tensione. Nei seguenti due paragrafi E2-2 e E2-3 sono riportate le relazioni per determinare il circuito equivalente di più bipoli passivi (di tipo resistivo, induttivo e capacitivo) connessi in serie e in parallelo; nel paragrafo E3-6b quelle per determinare i generatori equivalenti di Thevenin e di Norton.
Circuiti equivalenti serie
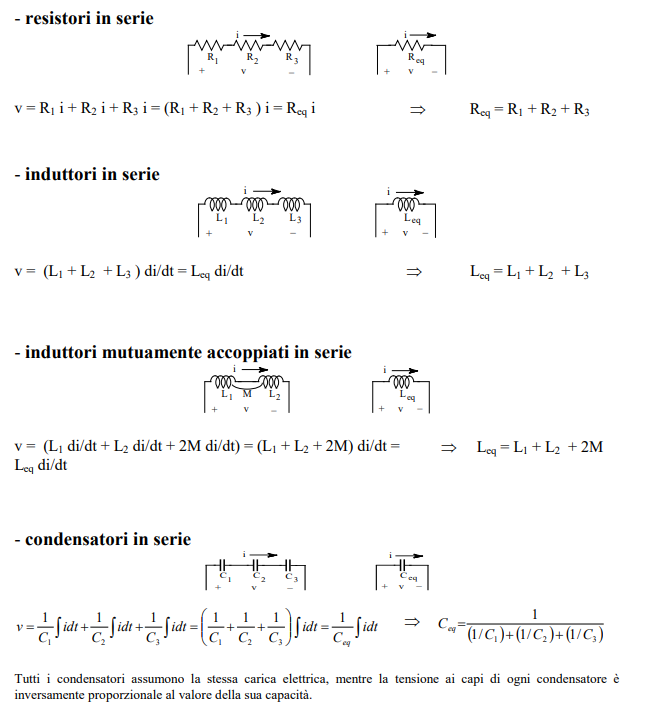
Circuiti equivalenti parallelo

Collegamenti a stella e a triangolo
Nel procedimento per la determinazione del circuito equivalente di una parte di rete passiva, nel caso in cui vi siano più bipoli non connessi né in serie né in parallelo, si ricorre alle trasformazioni triangolo-stella (∆-Y) o stella-triangolo (Y-∆) e quindi si procede con serie e parallelo. Una stella è un tripolo costituito da tre bipoli aventi un morsetto comune mentre i tre morsetti liberi sono collegati a punti di diverso potenziale. Un triangolo è un tripolo costituito da tre bipoli collegati uno di seguito all’altro in modo da formare una figura chiusa e i tre punti di connessione sono collegati a punti di diverso potenziale. Nelle figure E2-3a e E2-3b sono rappresentati i collegamenti rispettivamente a stella e a triangolo di tre bipoli resistivi.

Le equazioni che consentono di effettuare le trasformazioni (∆-Y e Y-∆) si ricavano estendendo ad un tripolo il concetto di equivalenza espresso per un bipolo. Un tripolo è equivalente ad un altro se, considerati due qualsiasi morsetti dell’uno, la relazione tra tensione applicata ai morsetti e corrente entrante è la stessa di quella che si ottiene considerando i morsetti corrispondenti dell’altro tripolo. Ciò equivale, imponendo l’equivalenza fra i due tipi di collegamento per ognuna delle tre coppie di nodi, ad impostare il seguente sistema di equazioni.

che risolto assumendo come incognite R1, R2, R3 fornisce la terna di equazioni che definiscono la trasformazione triangolo-stella (∆-Y)

mentre risolto assumendo come incognite R12, R23, R31 si ottiene la terna di equazioni che definiscono la trasformazione stella-triangolo (Y-∆)

Nel caso di tre resistenze uguali, posto R12=R23=R31=R∆ e R1=R2=R3=RY , le sei precedenti relazioni si riducono alla seguente:
R∆ = 3RY
In generale la resistenza equivalente di una qualsiasi parte di rete elettrica si può determinare come rapporto fra la tensione applicata tra i suoi due morsetti e la corrente entrante da uno dei due. La rete deve però essere passiva o resa tale disattivando tutti gli eventuali generatori presenti.