Risoluzione di Reti Elettriche

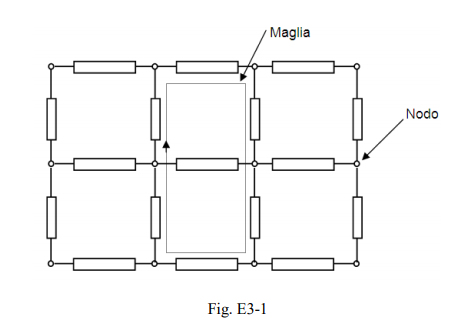
In figura E3-1 è rappresentata una generica rete elettrica composta da vari rami, nodi e maglie. Definiamo
– ramo un circuito caratterizzato da un dato valore dell’intensità di corrente
– nodo una qualsiasi superficie chiusa in cui confluiscono tre o più rami
– maglia un insieme di rami che formano una figura chiusa
– rete un insieme di maglie aventi rami in comune.

Le direzioni convenzionali di riferimento della tensione (il morsetto a potenziale maggiore è contrassegnato col segno +, l’altro col segno -) e della corrente (una freccia indica il verso in cui si muovono le cariche positive quando la corrente è positiva) associate ad ogni circuito vengono prefissate in maniera arbitraria e indipendentemente l’una dall’altra. Tuttavia ai fini pratici risulta conveniente scegliere il verso della corrente entrante dal morsetto contrassegnato col + quando il circuito è utilizzatore, il verso opposto quando il circuito è generatore. La distinzione è fondamentale ai fini della potenza elettrica; il prodotto v⋅i se ha segno positivo nella convenzione dell’utilizzatore fornisce la potenza assorbita dal circuito, in quella del generatore fornisce la potenza erogata dal circuito.

Principi di Kirchhoff

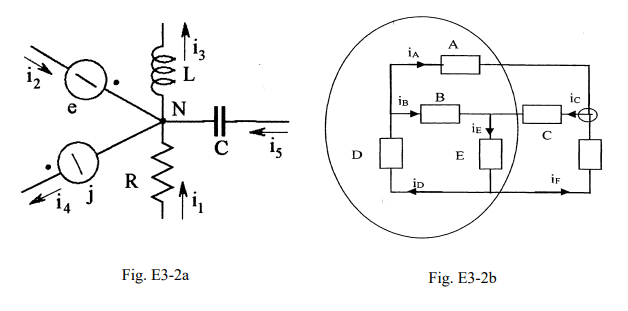
Primo principio di Kirchhoff: la somma delle correnti entranti in un nodo è uguale alla somma delle correnti uscenti; ciò in quanto in un nodo in condizione di regime stazionario non può aversi né accumulo né sottrazione di cariche elettriche. Più in generale la somma algebrica di tutte le correnti entranti in un nodo è zero.

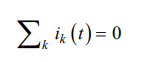
Per il nodo N di figura E3-2a si ha: i₁+i₂+i₅ = i₃+i₄ ; per la superficie chiusa di figura E3-2b si ha: i_C−i_A−i_F = 0.

Secondo principio di Kirchhoff: la somma algebrica delle f.e.m. che agiscono nei rami di una maglia di una rete elettrica è uguale alla somma algebrica delle cadute di tensione lungo i rami della stessa maglia

Le cadute di tensione Ri sono assunte positive se la corrente, nel ramo considerato, circola nel verso di percorrenza della maglia, negative in caso contrario; le f.e.m. sono assunte positive se, seguendo il verso di percorrenza della maglia, si entra dal morsetto negativo del generatore, negative in caso contrario. Le tensioni di lato incognite si calcolano poi successivamente con le equazioni costitutive.

Albero e coalbero

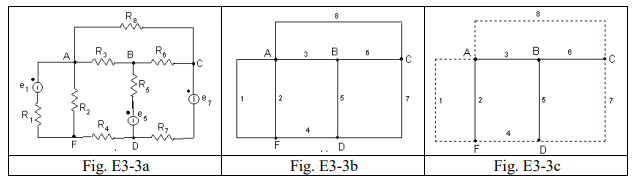
Se i rami di una rete (fig. E3-3a) vengono vengono sostituiti con linee si ottiene il cosiddetto grafo della rete (fig. E3-3b). Due reti diverse ma con lo stesso grafo sono caratterizzate dalle stesse equazioni di Kirchhoff
Un percoso che collega tutti i nodi del grafo, senza formare maglie, viene chiamato albero; i lati del grafo, che non fanno parte dell’albero, costituiscono il coalbero.
In figura E3-3c sono rappresentati un albero (lati a tratto continuo) ed il coalbero (lati tratteggiati) del grafo di figura E3-3b.

Man mano che ad un albero si aggiunge un lato del coalbero si forma una maglia; le maglie così individuate hanno la proprietà di avere un lato in esclusiva cioè non appartenente ad altre maglie. Come esempio si consideri la rete di figura E3-4a. Le 3 maglie indipendenti vengono individuate aggiungendo, ad uno degli alberi della rete, i lati del coalbero (figg. E3-4b e E3-4c).

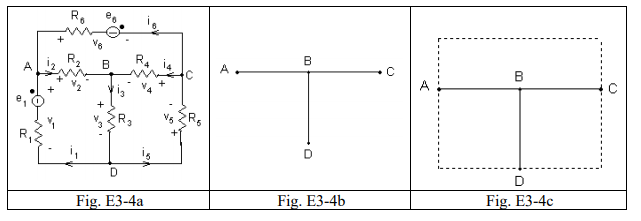
Se nella rete sono presenti generatori ideali di corrente, il criterio di scelta delle maglie indipendenti non cambia ma è opportuno che i generatori di corrente si trovino inseriti in lati del coalbero. Le equazioni alle maglie comprendenti generatori di corrente servono solo al calcolo della tensione ai morsetti di tali generatori.

Analisi dei circuiti

L’analisi di una rete con sollecitazioni e parametri noti consiste nel determinare le correnti che circolano nei vari rami e le differenze di potenziale tra punti generici. Per risolvere tale problema si possono utilizzare varie metodologie, tra cui
– il metodo delle correnti di ramo
– il metodo delle correnti di maglia
– il principio di sovrapposizione degli effetti
– il generatore equivalente di Thevenin.

Metodo delle correnti di ramo
Un modo per effettuare l’analisi di una rete comunque complessa, costituita da n nodi e r rami, consiste nell’impostare un sistema di r equazioni linearmente indipendenti, applicando i due principi di Kirchhoff, dopo aver attribuito arbitrariamente i versi convenzionali di riferimento per le correnti incognite.
Il primo principio di Kirchhoff si applica a n−1 nodi della rete. Il nodo n-esimo a cui non applicarlo (in quanto la relativa equazione non sarebbe significativa) è completamente arbitrario.
Il secondo principio di Kirchhoff si applica, dopo aver stabilito un verso di percorrenza positivo, a r−(n−1) maglie, scelte in modo che le equazioni risultino tra loro linearmente indipendenti; a tal fine è sufficiente che ogni maglia contenga almeno un lato non appartenente ad altre maglie. Per la scelta delle maglie conviene individuare un albero e quindi aggiungere i lati del coalbero. Si può anche usare il seguente procedimento: applicato il secondo principio di Kirchhoff ad una generica maglia, si interrompe un suo ramo prima di scegliere la successiva maglia a cui applicarlo e così di seguito fino a quando nella rete sono presenti percorsi chiusi.
I rami che contengono generatori di corrente vanno interrotti prima di applicare il metodo poiché in essi la corrente è nota e pari a quella imposta dal generatore. Risolvendo il sistema così impostato, si ricavano tutte le r correnti incognite della rete; le correnti che risultano negative scorrono in senso opposto a quello inizialmente attribuito in modo arbitrario.

Esempio. Per risolvere il circuito di figura E3-6 costituito da 6 rami e 4 nodi utilizzando i due principi di Kirchhoff dovremmo scrivere n −1= 3 equazioni ai nodi e r−(n−1) = 3 equazioni alle maglie. Nel caso di funzionamento a regime stazionario però, dato che sono nulle le d.d.p. tra i morsetti degli induttori percorsi da corrente costante (cortocircuiti) e le correnti nei condensatori alimentati a tensione costante (circuiti aperti), i₆ = 0 e quindi i₃ = i₅ = −i₄ ed è perciò sufficiente scrivere 1 equazione ai nodi e 2 equazioni alle maglie

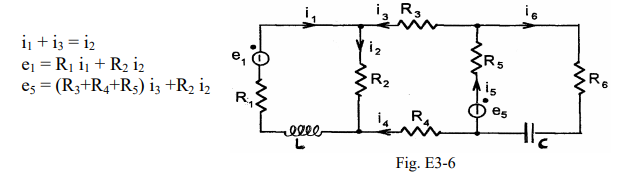
Risolvendo tale sistema si ricavano le correnti nei rami della rete e quindi si possono determinare le d.d.p. tra i vari nodi.

Metodo delle correnti di maglia
Il metodo delle correnti di ramo permette di risolvere qualsiasi rete comunque complessa. Se però il numero delle incognite è elevato per abbreviare il procedimento di calcolo conviene utilizzare il metodo delle correnti di maglia. Tale metodo consente infatti di impostare, utilizzando il secondo principio di Kirchhoff, un sistema ridotto costituito da r-(n-1) equazioni, aventi come incognite delle correnti fittizie che fluiscono nelle singole maglie indipendenti della rete; in funzione di tali correnti fittizie si ricavano poi in maniera semplice e rapida tutte le r correnti incognite reali.

Operativamente si procede nel seguente modo:
– si individuano tutte le maglie indipendenti e si attribuiscono loro correnti fittizie aventi (non obbligatoriamente) tutte lo stesso verso (orario o antiorario) convenzionalmente scelto come positivo;
– si scrivono le equazioni alle maglie in funzione di tali correnti fittizie (nelle maglie in cui è presente un generatore di corrente la corrente è quella imposta dal generatore stesso) e si risolve il sistema ottenuto;
– si determinano infine le correnti reali in ogni ramo, effettuando la somma algebrica delle correnti fittizie relative a quel ramo

L’equazione relativa ad ogni singola maglia è strutturata nel seguente modo
– il primo membro è costituito dalla somma algebrica delle tensioni dei generatori di tensione presenti nella maglia, il cui segno è positivo o negativo a seconda che la loro polarità sia tale da fare circolare la corrente di maglia nel senso convenzionalmente assunto come positivo o no;
– il secondo membro è costituito da un termine positivo, ottenuto dal prodotto della corrente fittizia circolante nella maglia per la somma di tutte le resistenze presenti nella maglia, e da tanti termini negativi, ottenuti come prodotti delle correnti fittizie circolanti nelle maglie contigue per le resistenze dei rami a comune.

Per esempio, nel caso del circuito di figura E3-7 per determinare le sei correnti di ramo, è sufficiente risolvere il seguente sistema di tre equazioni che ha come incognite le correnti di maglia i_a i_b i_c.

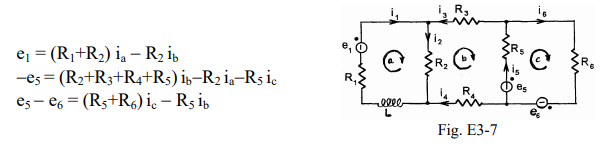
Ciò fatto le correnti di ramo valgono

Principio di sovrapposizione degli effetti

In una rete composta da elementi lineari dove agiscono più generatori di tensione e/o corrente la corrente in un ramo (o la d.d.p. tra due punti) è pari alla somma delle correnti (o delle d.d.p.) che i singoli generatori vi produrrebbero agendo separatamente.

Risulta essere possibile quindi determinare l’intensità della corrente in un ramo (o della d.d.p. tra due punti generici) di una rete procedendo nel seguente modo
1) si scompone la rete in esame in tanti reti parziali (quanti sono i generatori) aventi ciascuna tutti i generatori disattivati tranne uno
2) si calcola per ognuna di queste reti la corrente nel ramo desiderato (o la d.d.p. tra i due punti di interesse)
3) si sommano algebricamente i valori parziali delle correnti in quel ramo (o delle d.d.p. tra quei due punti).

Un generatore ideale di tensione è disattivato quando tensione ai suoi morsetti è nulla, ossia quando è in corto circuito; pertanto per annullare l’azione di un generatore di tensione reale si deve cortocircuitare la sua forza elettromotrice lasciando inserita la sua resistenza interna in serie. Un generatore ideale di corrente è disattivato quando eroga corrente nulla, ossia quando è un circuito aperto; pertanto per annullare l’azione di un generatore di corrente reale si deve aprire il ramo che lo contiene lasciando inserita la sua resistenza interna in parallelo.

Generatore equivalente di Thevenin

In base al teorema di Thevenin, una parte di rete lineare comunque complessa, comprendente resistori e generatori di tensione e/o di corrente, e con due morsetti accessibili (A e B) può essere sostituita con un generatore reale di tensione, detto generatore di Thevenin, la cui f.e.m. E_Th è uguale alla d.d.p. tra i morsetti A e B a vuoto (cioè in assenza della restante parte della rete o circuito esterno) e la cui resistenza interna R_Th è uguale a quella vista dagli stessi morsetti A e B sempre in assenza del circuito esterno e con la rete resa passiva disattivando tutti i generatori presenti.

Analogia tra circuiti magnetici e circuiti elettrici

Nella tabella E3-1 sono poste in corrispondenza grandezze e leggi relative a circuiti elettrici e magnetici, da cui si possono notare le notevoli analogie esistenti tra tali circuiti.

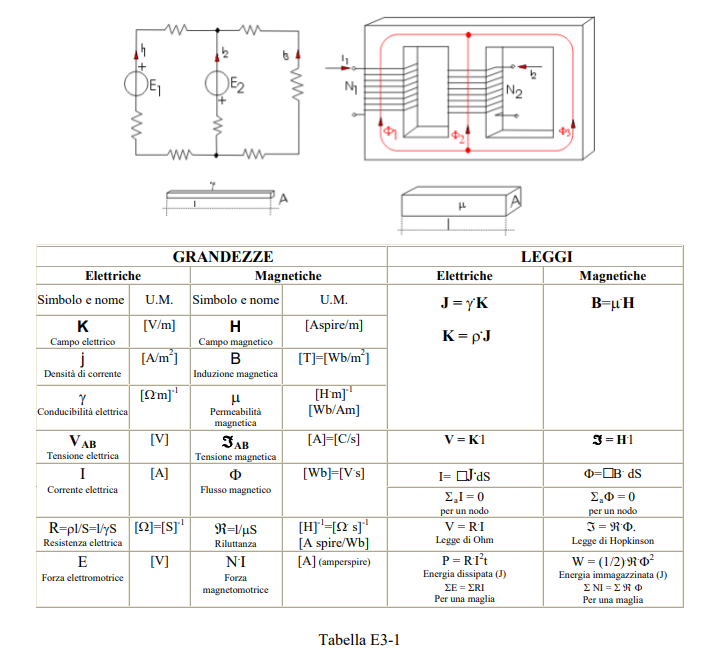
Così ad esempio
– note le dimensioni geometriche e le caratteristiche magnetiche di un generico circuito magnetico, è possibile scomporlo in più tronchi (regioni a permeabilità e sezione costante) ognuno caratterizzato da una propria riluttanza che nell’analogia magneto-elettrica corrisponde ad una resistenza;
– note poi il numero di spire delle varie bobine disposte sul circuito magnetico e l’ampiezza e il verso delle correnti che le percorrono è possibile determinare entità e polarità delle varie f.m.m. che nell’analogia magneto-elettrica corrispondono a generatori di tensione.

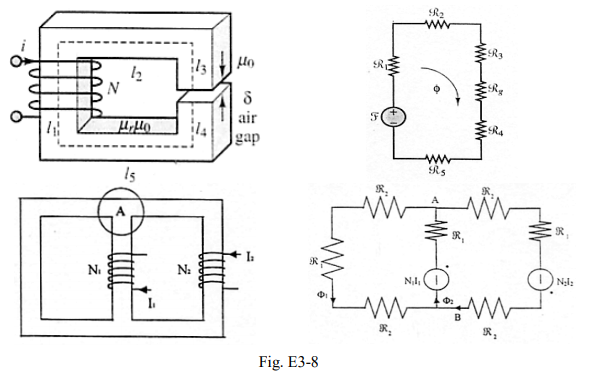
Determinato perciò il circuito elettrico equivalente (fig. E3-8), l’analisi di un circuito magnetico può essere effettuata utilizzando leggi e relazioni analoghe a quelle dei circuiti elettrici (legge di Ohm, principi di Kirchhoff, circuiti equivalenti serie parallelo, ecc.).

Una differenza fondamentale tra circuiti magnetici ed elettrici deriva dalle differenti caratteristiche funzionali determinate rispettivamente dalla permeabilità magnetica µ dei materiali ferromagnetici e dalla conducibilità γ dei materiali conduttori:
– la permeabilità µ è infatti molto variabile al variare della f.m.m., mentre la conducibilità γ è praticamente costante al variare della d.d.p.;
– non esistono materiali magnetici la cui permeabilità possa ritenersi praticamente nulla rispetto a quella dei materiali ferromagnetici, mentre la conducibilità degli isolanti può ritenersi praticamente nulla rispetto a quella dei materiali conduttori; per cui la presenza di un tratto in aria in un circuito magnetico comporta una riduzione del flusso, mentre in un circuito elettrico l’annullamento della corrente.