Indice
L’enunciato di Fourier afferma: “Qualunque segnale periodico è scomponibile nella somma di un eventuale termine costante (corrispondente al valore medio del segnale) e di una serie (in genere infinita) di segnali sinusoidali dei quali uno ha la stessa frequenza del segnale considerato (prima armonica o fondamentale) e gli altri hanno frequenze multiple intere (armoniche superiori) con ampiezze via via decrescenti”.
Questa esercitazione ha appunto lo scopo di visualizzare il principio affermato da Fourier. A questo scopo creiamo alcuni dei principali segnali periodici che sono comuni in elettronica: dente di sega, onde rettangolari o quadre e triangolari.
Prima di partire ricordiamo alcune cose, l’enunciato di Fourier si può esprimere con la seguente espressione
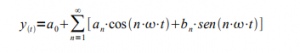
nella quale il termine costante a0 rappresenta il valor medio del segnale y(t), mentre an e bn sono i termini moltiplicativi, via via decrescenti, delle funzioni seno e coseno a frequenze via via crescenti. Se il segnale ha valor medio nullo, ossia è un segnale “alternato”, il termine noto avrà valore nullo. Se la funzione poi è “dispari”, ossia è simmetrica rispetto all’origine degli assi, sono nulli i termini coseno.
Nei altri casi i segnali possono essere di tipo “unipolare” o “bipolare”, di tipo “pari” oppure “né pari né dispari”. Per ulteriori chiarimenti si può consultare la nota esplicativa alla fine di questo documento.
Onda a Dente di Sega (Saw-Tooth)
Il segnale che vogliamo rappresentare è il seguente, si tratta quindi di un segnale bipolare o alternato (non ha quindi termine noto), inoltre è di tipo dispari (non ha quindi i termini di tipo coseno ma solo quelli di tipo seno).
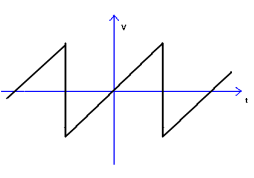
Evitando la parte puramente matematica che è di particolare complessità arriviamo subito all’espressione che rappresenta il segnale desiderato, cioè alla sommatoria di una serie infinita di termini.
Secondo l’enunciato di Fourier quindi l’onda a dente di sega si può rappresentare con questa serie
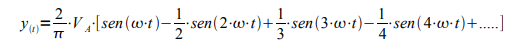
osserviamo che i termini sono alternativamente positivi e negativi ed hanno frequenze crescenti ed ampiezze decrescenti. Possiamo quindi ricreare questo segnale con una serie di generatori sinusoidali, collegati in serie e che sommano i loro contributi per generare il segnale finale. E’ preferibile mettere tutti i generatori in serie rispettando le polarità e quindi mettere il segno negativo al valore da attribuire all’ampiezza, in modo da sottrarre il suo contributo dalla serie.
Per comodità riportiamo in una tabella i valori da attribuire ai vari parametri dei generatori.
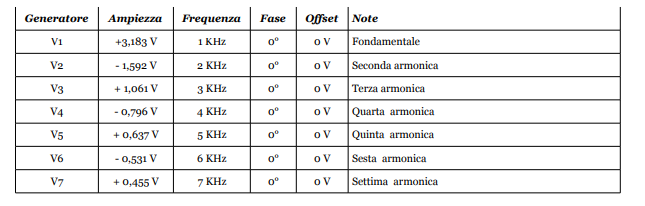
Questi valori sono stati calcolati per una forma d’onda a dente di sega con periodo di 1 msec e quindi frequenza di 1 Khz ed ampiezza di 5 volt, che in Pspice significa che la tensione varia da -5V a +5V.
Per generare il segnale di riferimento utilizziamo un generatore VPULSE impostando questi parametri.

Per osservare meglio il procedere della serie di somme è conveniente utilizzare nello schema vari circuiti come illustrato in figura, si vedrà così il segnale a dente di sega da creare come risultato finale (questo segnale è generato da VPULSE) e si vedranno anche i risultati della sommatoria con un solo termine della serie, quindi con due termini, con tre termini e così via.
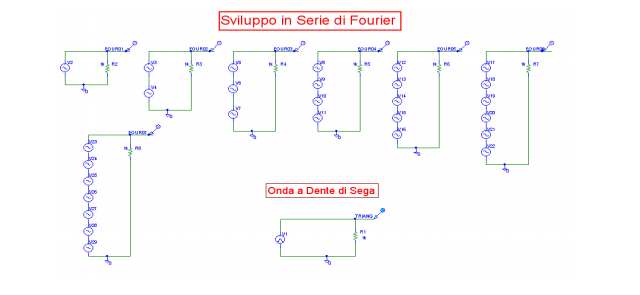
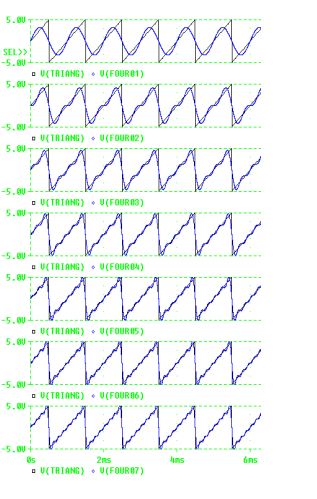
Lanciamo la simulazione e vediamone il risultato, sovrapponendone opportunamente i vari risultati intermedi.
Come si può vedere, via via che si aggiungono termini alla serie la forma d’onda risultante (in colore blu) si approssima sempre di più alla forma a dente di sega (in colore nero) che volevamo realizzare.
Possiamo quindi affermare che la dimostrazione del teorema dello sviluppo in serie di Fourier è pienamente riuscita.
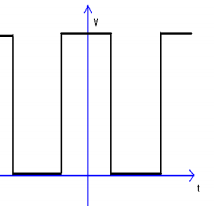
Onda Quadra o Rettangolare
Il segnale che vogliamo rappresentare è il seguente, si tratta quindi di un segnale ad onda quadra unipolare (ha quindi un termine noto a sommare), di tipo pari perché è simmetrico rispetto all’asse delle ordinate (ha quindi solo i termini di tipo coseno).
La funzione risultante del segnale desiderato è quindi rappresentata dalla seguente sommatoria nella quale come al solito i vari coefficienti hanno alternativamente il segno positivo e quello negativo.
Da notare che nella serie abbiamo solo le armoniche dispari della fondamentale
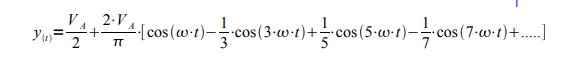
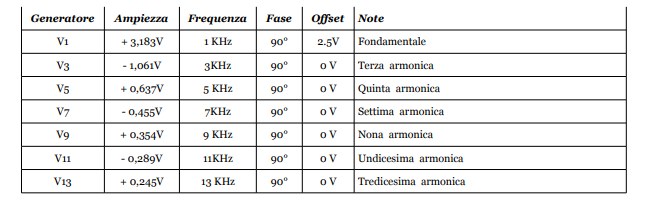
Come nel caso precedente per comodità riportiamo in una tabella i valori da attribuire ai vari parametri dei generatori. Da notare che la fase è sempre 90° trattandosi di termini coseno e che l’offset del primo generatore corrisponde al valore del termine noto, ossia al valore medio del segnale risultante. Ricordiamoci anche della differenza dei termini per onda quadra (duty cycle del 50%) e rettangolare (duty cycle diverso dal 50%).
Fermiamoci anche qui al 7° elemento della sommatoria, come approssimazione può essere più che sufficiente.
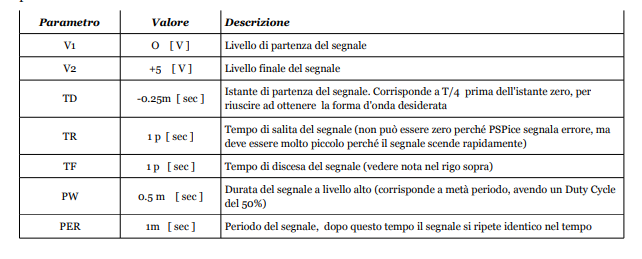
Questi valori sono stati calcolati per una forma d’onda quadra con periodo di 1 msec e quindi frequenza di 1 Khz ed ampiezza di 5 volt, utilizziamo quindi un generatore VPULSE impostando questi parametri
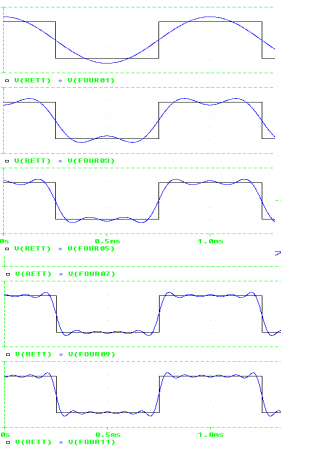
Lanciamo la simulazione e vediamone il risultato, sovrapponendone opportunamente i vari risultati intermedi.
Come si può vedere, via via che si aggiungono termini alla serie la forma d’onda risultante (in colore blu) si approssima sempre di più alla forma d’onda quadra (in colore nero) che volevamo realizzare. Nonostante siano stati utilizzati solo 6-7 termini il risultato è eccellente.
Possiamo quindi affermare che, anche in questo caso, la dimostrazione del teorema dello sviluppo in serie di Fourier è pienamente riuscita.
Onda Triangolare
Il segnale che vogliamo rappresentare è il seguente, si tratta quindi di un segnale bipolare alternato (non ha quindi un termine noto a sommare), inoltre è di tipo pari perché è simmetrico rispetto all’asse verticale (ha quindi solo i termini di tipo coseno).
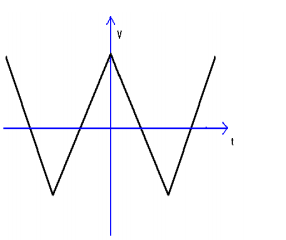
La funzione risultante del segnale desiderato è quindi rappresentata dalla seguente sommatoria nella quale notiamo che le ampiezze vanno rapidamente decrescendo poiché al denominatore compare il termine n2 , dove n è rappresentato solo dai coefficienti dispari.
Anche in questo caso nella serie abbiamo solo le armoniche dispari della fondamentale.
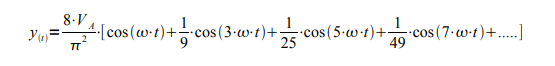
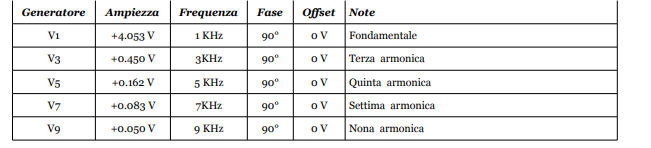
Come nel caso precedente per comodità riportiamo in una tabella i valori da attribuire ai vari parametri dei generatori. La fase è sempre 90° trattandosi di termini coseno e che l’offset del primo generatore corrisponde al valore del termine noto, ossia al valore medio del segnale risultante.
In questo caso possiamo fermarci molto prima, ad esempio al 5° elemento della sommatoria, come approssimazione può essere più che sufficiente, visto che l’ampiezza qui cala molto velocemente.
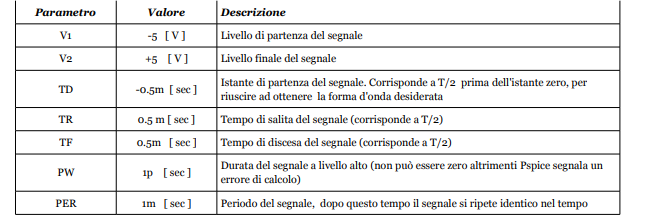
Questi valori sono stati calcolati per una forma d’onda triangolare con periodo di 1 msec e quindi frequenza di 1 Khz ed ampiezza che spazia dai -5 V ai +5 V, utilizziamo quindi un generatore VPULSE impostando questi parametri
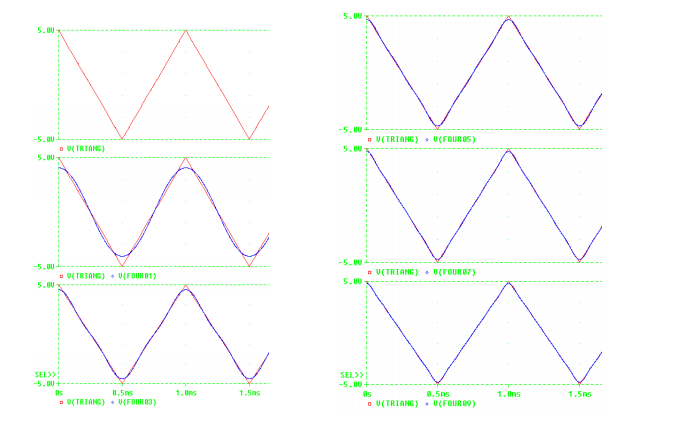
Lanciamo la simulazione e vediamone il risultato, sovrapponendone opportunamente i vari risultati, anche in questo caso il risultato è ottimo.