Indice
Nei componenti passivi (resistori) e a semiconduttore (sia discreti che integrati) il passaggio della corrente elettrica provoca – per effetto Joule – un innalzamento della temperatura dei dispositivi, che può essere calcolato attraverso la seguente relazione
(1) Tw – Ta = Pd · Rth
dove Tw è la temperatura raggiunta dal dispositivo a causa della dissipazione della potenza applicata Pd, Ta è la temperatura dell’ambiente circostante ed Rth è una costante che viene chiamata “resistenza termica”, che rappresenta la difficoltà di smaltimento del calore verso l’ambiente circostante ed è l’inverso della “conduttanza termica” dei materiali e dei fluidi che smaltiscono il calore prodotto. Dalla (1) si ricava che l’unità di misura della resistenza termica è il grado/Watt (°C/W).
Poiché il costruttore del dispositivo indica nel foglio tecnico una temperatura massima di funzionamento Tmax, è possibile calcolare la massima potenza Pmax dissipabile dal dispositivo stesso ad una temperatura ambiente Tamax sfruttando la relazione, e riscrivendola nel modo seguente
(2) Tmax – Tamax = Pmax · Rth
La relazione ora vista ci spiega inoltre perché, una volta raggiunta la massima temperatura specificata, un’ulteriore incremento della potenza applicata porterebbe ad un ulteriore aumento della temperatura, con conseguente possibile danneggiamento del dispositivo. Dovrebbe essere chiaro, quindi, che i limiti di potenza specificati per un certo dispositivo dipendono strettamente dai limiti di temperatura dello stesso.
La curva di derating
Nel foglio tecnico di un resistore viene riportato un grafico detto “curva di derating”, mostrato in Figura 1
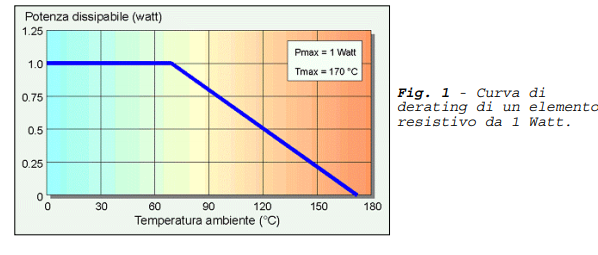
Come si vede dalla curva di derating, è possibile dissipare la potenza nominale fino ad una temperatura ambiente di 70 °C, superata la quale è necessario ridurre progressivamente la potenza dissipata fino a che – raggiunta la temperatura massima di lavoro di 170 °C – la potenza dissipabile diviene nulla come già osservato a proposito della relazione . Vi è da notare però che la rappresentazione grafica della relazione in un piano di coordinate Pd/Ta è quella di una retta di coefficiente angolare -1/Rth, e non quello di una spezzata come quella riportata in Figura 1. Perché mai? La risposta è che il costruttore, per problemi legati alle caratteristiche dei materiali utilizzati nella costruzione del dispositivo, indica una potenza massima dissipabile “di sicurezza” fino ad una determinata temperatura ambiente, che nella figura riportata è ad esempio di 70 °C. Secondo la relazione avremmo invece che a temperature inferiori allo zero potremmo in teoria dissipare potenze progressivamente crescenti, ciò che il costruttore ci sconsiglia di fare.
I dissipatori e i meccanismi di propagazione del calore
Visti i limiti di temperatura – e quindi di potenza – imposti dal costruttore (e utili alla corretta “sopravvivenza” del dispositivo!) come è possibile smaltire adeguatamente il calore prodotto o addirittura estendere i limiti indicati dalla curva di derating? Per i dispositivi di potenza la risposta è semplice: l’impiego del “dissipatore di calore”, ovvero di un elemento che sia un buon conduttore di calore (tipicamente un metallo o un materiale ceramico) che, posto a contatto con il nostro dispositivo (incollato o fissato a vite), permetta un migliore smaltimento del calore. Come opera un dissipatore? In pratica esso “estende” le dimensioni fisiche del dispositivo, permettendo quindi un miglior smaltimento del calore, in quanto “sottrae” il calore prodotto per effetto Joule e lo trasferisce all’ambiente circostante, e impedisce il superamento della temperatura limite.
Che cosa cambia nella formula (2)? Semplice: poiché la presenza del dissipatore serve per aumentare la conduttanza termica fra il nostro dispositivo e l’ambiente, si può affermare che la presenza del dissipatore porta ad una riduzione della resistenza termica, che è appunto l’inverso della conduttanza termica. La riduzione della Rth nella formula (2) permette quindi di diminuire la temperatura raggiunta dal dispositivo oppure – volendo sfruttare comunque la massima temperatura di lavoro – disporre di una potenza dissipabile più elevata.
Per meglio comprendere non solo il meccanismo di smaltimento del calore ma anche come ottimizzare i vantaggi derivabili dall’impiego di un dissipatore, analizziamo brevemente le tre modalità di propagazione del calore.
– Conduzione: è quella che avviene all’interno di un corpo o fra due corpi in contatto fra di loro a causa dell’agitazione termica degli atomi, ed è il meccanismo più efficiente di trasmissione del calore. Per tale motivo il dispositivo che produce calore va fissato saldamente a contatto con il dissipatore, che deve essere costituito da un materiale con una elevata conducibilità termica; il materiale più utilizzato grazie al costo contenuto e alla facilità di produrre profilati ottenuti per estrusione è l’alluminio.
– Convezione: la convezione è il moto all’interno di un fluido, per cui si sfrutta questo fenomeno ad esempio per asportare il calore del dissipatore (o del componente stesso) attraverso il movimento dell’aria, che può essere naturale (dovuto al fenomeno di espansione termica) oppure forzato (tramite ventole). Per le elevate potenze, il fluido refrigerante può essere anche un liquido, che scorre in un condotto all’interno del dissipatore e viene poi raffreddato o per sostituzione (acqua corrente) o tramite un opportuno radiatore.
– Irraggiamento: il dissipatore e lo stesso componente irradiano calore nell’ambiente circostante per mezzo della radiazione infrarossa, ed anche questo fenomeno contribuisce allo smaltimento del calore, anche se alle basse temperature rappresenta una frazione trascurabile del totale. Una esemplificazione visiva dei tre meccanismi è mostrata in Figura 2.
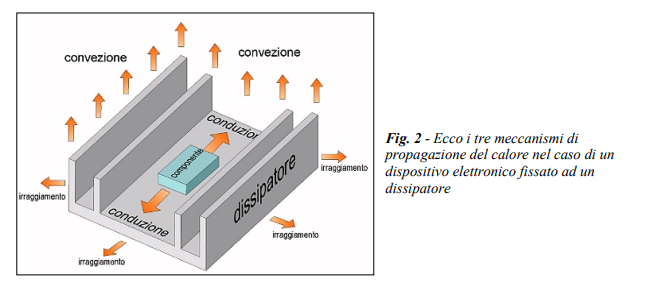
Va inoltre precisato che l’efficienza di un dissipatore dipende da parametri quali ad esempio il materiale utilizzato (conducibilità termica), le sue dimensioni (valore della resistenza termica), la forma (efficacia della convezione dell’aria), il colore (effetto “corpo nero” e quindi efficienza nell’irraggiamento), la finitura superficiale (resistenza di contatto con il componente elettronico e valore dell’irraggiamento), le condizioni di ventilazione (anche se interno o esterno all’apparecchiatura), la posizione di montaggio (verticale ad alette verticali per una migliore convezione dell’aria) e infine la posizione di montaggio del carico sul dissipatore stesso (centrale oppure verso il bordo). Detto ciò, il parametro che caratterizza l’efficienza di un dissipatore e che riassume gli altri parametri ora visti è la sua resistenza termica Rth(d-a), ovvero fra dissipatore e ambiente, che viene specificata dal costruttore sul relativo foglio tecnico, e che viene definita come l’incremento di temperatura subito a causa dell’applicazione di una potenza elettrica (attiva) di 1 Watt, concordemente con quanto si può dedurre dalla relazione (1)
La scelta del dissipatore
Per scegliere un dissipatore occorre conoscere i seguenti parametri
– Potenza massima dissipata dal dispositivo
– Temperatura massima consentita per il dispositivo e sua resistenza termica
– Massima temperatura ambiente
– Tipo di flusso di aria in corrispondenza del dissipatore
Per tener conto di questi parametri, la formula (2) può essere riscritta nel modo seguente, facendo riferimento ad un dispositivo a semiconduttore
(3) Tjmax – Tamax = Pdmax · (Rthjc + Rthcd + Rthda)
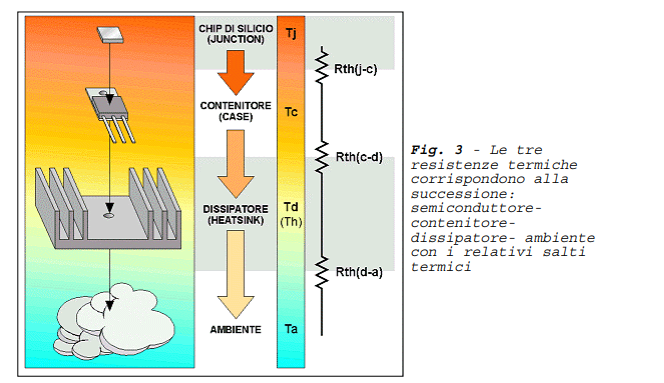
dove Tjmax è la massima temperatura di giunzione specificata dal costruttore, Tamax è la massima temperatura ambiente raggiungibile, Pdmax è la potenza massima dissipabile, Rthjc è la resistenza termica fra giunzione e contenitore (indicata dal costruttore sul foglio tecnico del dispositivo), Rthcd è la resistenza termica fra contenitore e dissipatore (dovuta al tipo di contatto fra i due e alla eventuale presenza di fogli isolanti o di grasso) ed Rthda è la resistenza termica dissipatore-ambiente ricavata dal catalogo dei dissipatori. La localizzazione delle tre resistenze termiche è mostrata in Figura 3.
Nel caso invece in cui si intenda utilizzare il componente senza dissipatore, è necessario utilizzare la formula seguente, che rappresenta nient’altro che una riscrittura della (2)
(4) Tjmax – Tamax = Pdmax · Rthja
nella quale si utilizza la sola resistenza termica giunzione-ambiente Rthja fornita anch’essa nel foglio tecnico del componente.
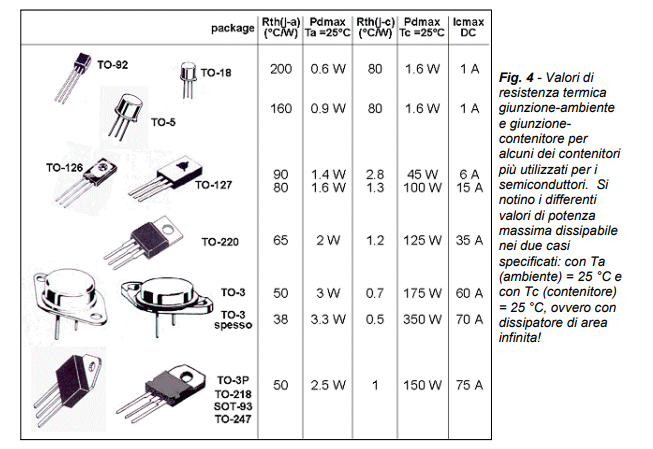
Nella Figura 4 sono riportati i valori di resistenza termica Rthjc ed Rthja per alcuni dei più comuni contenitori impiegati in elettronica per i dispositivi a semiconduttore.
Equivalenza dei modelli termico ed elettrico
Ragionando più a fondo su quanto finora detto si può affermare che il modello “termico” di elemento che dissipa potenza per effetto Joule presenta strette analogie con l’equivalente elettrico, al punto che si può fornire una descrizione in termini circuitali del fenomeno di scambio termico fra elemento che produce dissipazione, le resistenze termiche, le varie temperature ed il flusso di calore. Tale modello è rappresentato nello schema seguente.
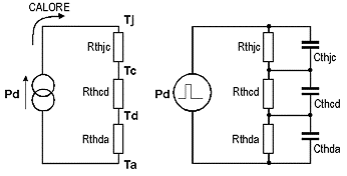
Nel caso di potenza continua applicata la “corrente” che fluisce nel circuito è costituita dal flusso di calore, il quale provoca, ai capi delle “resistenze termiche” una “differenza di temperatura” (invece che di tensione); nella pratica, quindi, più elevata è la resistenza termica del dissipatore, tanto più elevata sarà la temperatura del dissipatore, che non permetterà un sufficiente raffreddamento del componente. Nel caso invece in cui la potenza applicata sia del tipo a impulsi entrano in gioco anche le “capacità termiche” (l’unità di misura è il Joule/°C) che sono connesse in parallelo alle rispettive resistenze termiche. Risulta essere quindi evidente il motivo per cui se la potenza applicata varia nel tempo la “reattanza” delle capacità termiche essendo in parallelo alle resistenze termiche ne riduce il valore, in maniera proporzionale alla riduzione della durata degli impulsi.
Varie resistenze termiche
Vi è però da tener conto che, nel caso in cui il componente elettronico sia incapsulato in un contenitore che consenta il fissaggio a un dissipatore, la formula (2) va scritta in un modo più complesso, in quanto dovrà tener conto delle differenti resistenze termiche che il flusso di calore incontra nel suo propagarsi dal chip di silicio al contenitore, da questo al dissipatore, e da questo all’ambiente, proprio come illustrato in modo schematico in figura 3. In sostanza, nel caso in cui si usi il dissipatore, la sequenza di ciò che il calore incontra nel suo propagarsi dal chip (dove esso si origina per effetto Joule) e l’ambiente (che si trova a più bassa temperatura e quindi in grado di “assorbire” il calore) può essere rappresentata come nella figura 3, dove sono appunto indicate le tre resistenze termiche, e precisamente: Rt(j-c) [resistenza termica fra giunzione e contenitore] fornita dal costruttore e che dipende dalle modalità costruttiva del dispositivo e dai materiali utilizzati, Rt(c-d) [resistenza termica fra contenitore e dissipatore] che dipende dal modo di fissaggio del componente al dissipatore ed Rt(d-a) [resistenza termica fra dissipatore e ambiente detta anche semplicemente “resistenza termica del dissipatore”] che dipende dalla forma, dimensione, posizione ed eventuale ventilazione del dissipatore.
Si tenga conto che, mentre la resistenza termica del dissipatore Rth(d-a) può essere derivata dai manuali forniti dai costruttori dei dissipatori stessi, il valore della Rt(c-d) dipende dal tipo di fissaggio fra componente e dissipatore. Il valore di questa resistenza può variare in maniera significativa, e negli esempi che seguono utilizzeremo valori medi per fissaggi senza isolante su dissipatori con superfici lisce. A causa di quanto detto, la resistenza termica totale che il calore incontra nel suo propagarsi dalla giunzione all’ambiente è quindi costituita dalla somma delle tre resistenze suddette, ovvero
(3) R(j-a) = Rt(j-c) + Rt(c-d) + Rt(d-a)
quindi la (2), nel caso di impiego del dissipatore, deve essere riscritta nel modo seguente:
(4) Tj – Tamb = Pd · [Rt(j-c) + Rt(c-d) + Rt(d-a)]
e in essa andranno messi i relativi valori di Rt
Esempio di Calcolo Dissipatore
Facciamo un esempio. Supponiamo di utilizzare il transistor TIP131, ospitato nel contenitore TO-220, riportato qui a lato. Il costruttore dichiara sul foglio tecnico che esso può dissipare una potenza massima di 40W (a patto che il contenitore non superi i 25°C), ammette una Tj massima di 150°C ed è caratterizzato da una Rt(j-c) paria a 3.1 °C/W. La precisazione “a patto che il contenitore non superi i 25°C” ci fa immaginare che, per poter garantire tale condizione, dobbiamo raffreddare per bene il nostro transistor (il dissipatore è quindi indispensabile), altrimenti il contenitore si scalderà sicuramente e addio potenza di 40 watt! Supponiamo invece che il nostro transistor si trovi in un circuito in cui debba dissipare una potenza di soli 5 W racchiuso in un contenitore (il suo “ambiente”) con una temperatura di 40°C. Ci vorrà il dissipatore? Se si, come dovrà essere? Per scoprirlo è sufficiente utilizzare la (4), in cui supponiamo di fissare il contenitore al dissipatore con una Rt(c-d) di 0.9 °C/W e decidendo di sfruttare al massimo la giunzione di silicio, facendogli raggiungere i suoi 150 °C massimi. La formula diverrà quindi:
(5) 150 – 40 = 5 · [3.1 + 0.9 + Rt(d-a)]
da cui si ricava una resistenza termica dissipatore-ambiente di 18 °C/W. Dai fogli tecnici del costruttore di dissipatori si possono scegliere vari tipi di alette di raffreddamento, a seconda dell’ingombro voluto. Immaginiamo di scegliere un semplice tipo a “C”, visibile qui a lato. Esso misura 2 x 2 x 3 cm, è sufficiente per il TO-220 e presenta una resistenza termica di 14 °C/W, quindi inferiore ai 18 richiesti. Si noti che è preferibile che sia inferiore, e non maggiore: in tal modo conduce il calore meglio del dovuto, altrimenti si rischia il surriscaldamento del transistor! Si parla in questo caso di dissipatore “sovradimensionato”.
Grazie ai 14 °C/W di resistenza termica, il dissipatore scelto può permetterci di dissipare un po’ più dei 5 watt suddetti; inserendo infatti questo valore nella (5) si ha: 150 – 40 = Pd · [3.1 + 0.9 + 14] da cui si ottiene una potenza massima dissipabile di 6.1 W, ciò che ci fa ritenere che i nostri 5 W siano dissipabili in tutta sicurezza.
Non solo, ma a ben pensarci, possiamo anche intuire che dissipando solo 5 W anziché i 6.1 ammissibili il transistor lavorerà ad una temperatura inferiore ai 150 °C massimi. Si, ma a quanto? Lo possiamo scoprire sempre usando opportunamente la (5), e utilizzando come incognita proprio Tj, nel modo seguente: Tj – 40 = 5 · [3.1 + 0.9 + 14] ricavando che, grazie al dissipatore leggermente sovradimensionato, la temperatura interna del transistor raggiungerà i 130 °C anziché i 150 massimi, a tutto vantaggio della sicurezza di funzionamento e quindi della durata del componente.
Sapendo sfruttare per bene la formula (4) si possono ottenere anche altre informazioni utili, come ad esempio calcolare la temperatura assunta dal dissipatore. Come si fa? E’ semplice, basta riscrivere la formula relativamente al solo salto termico fra ambiente e dissipatore, in modo da trasformarla nella seguente
(6) Td – Tamb = Pd · Rt(d-a)
e sostituire i valori noti, con incognita proprio Td, e precisamente: Td – 40 = 5 · 14 dalla quale si ricava che il dissipatore raggiungerà i 110 °C, utile ad esempio se si intende minitorare la temperatura raggiunta dal dissipatore tramite dei sensori termici, spesso impiegati al fine di limitare la potenza dissipata (e quindi la temperatura raggiunta) ad esempio con dei contatti bimetallici o con dei termistori collegati a dei relè i quali, superata la soglia voluta, spengono il circuito. Si noti che lo stesso risultato può essere ottenuto anche effettuando il percorso inverso, ovvero partendo dalla temperatura del chip e dalla somma delle resistenze termiche per raggiungere il dissipatore, ovvero:
(7) Tj – Td = Pd · [Rt(j-c) + Rt(c-d)]
dove, sostituendo i valori, si ottiene
130 – Td = 5 · [3.1 + 0.9]
ottenendo comunque i 110 °C di prima
Se il nostro transistor avesse dovuto invece dissipare una potenza più elevata, avremmo dovuto utilizzare un dissipatore più grande, il quale viene però caratterizzato non già tramite un valore di resistenza termica definito, bensì tramite un grafico, quale ad esempio quello sottostante. Il motivo è che dissipatori di questo tipo vengono venduti in barre estruse, che possono essere tagliate in modo da ottenere il valore di resistenza termica voluto.
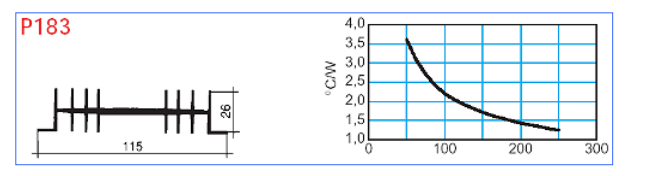
Per quello riportato in figura, per esempio (un dissipatore alettato estruso da 115 x 26 mm) la resistenza termica va dagli 1.2 ai 3.6 °C/W a seconda che la lunghezza scenda dai 25 ai 5 centimetri. E’ ovvio infatti che, più ridotte sono le dimensioni, più difficoltoso sarà lo smaltimento del calore, e quindi più elevata la resistenza termica. Domanda: se avessimo utilizzato questo dissipatore a tutta lunghezza per il nostro transistor dell’esempio precedente, che potenza avremmo potuto dissipare? Semplice, inseriamo nella (4) il valore di Rt(d-a) pari a 1.2 °C/W, in modo da ottenere: 150 – 40 = Pd · [3.1 + 0.9 + 1.2] dalla quale si ricava una potenza dissipabile di 21.1 watt contro i 5 W consentiti dal dissipatore a C.
Ma allora quando si potranno raggiungere i 40 W massimi dichiarati? Osserviamo innanzitutto che nell’esempio scelto l’ipotesi di partenza era che il nostro transistor si trovasse purtroppo ad operare in un contenitore a 40 °C e non in aria libera. In questo secondo caso la (4) fornirebbe una potenza dissipabile di: 150 – 25 = Pd · [3.1 + 0.9 + 1.2] ovvero di 24 watt, ma ancora ben lontani dai 40 dichiarati. Come mai? La risposta va trovata proprio nella precisazione del foglio tecnico: “potenza massima solo se il contenitore si trova a 25 °C”. Certo, ma se ci pensiamo, quando mai il package sarà esattamente alla temperatura ambiente? In pratica mai, in quanto proprio la (4) ci spiega che, per garantire ciò, sarebbe necessario usare un dissipatore di resistenza termica nulla, ovvero di area infinita, per cui possiamo dedurre che i 40 W rappresentano un limite teorico.
Non solo, ma per azzerare la somma [Rt(c-d) + R(d-a)] occorre anche che la resistenza termica contenitore-dissipatore sia nulla, contro i nostri 0.9 °C/W, che di fatto ci “mangiano”, a conti fatti, ben 5W! Infatti, se poniamo a zero la Rt(c-d) otteniamo una Pd di 29 W, ovvero 5 W in più. Per ottenere i 40 W teorici, dobbiamo quindi azzerare sia la resistenza termica del dissipatore sia quella del contatto fra contenitore e dissipatore, in modo che la relazione divenga: 150 °C – 25 °C = 40 W · 3.1 °C/W dove ci accorgiamo che i valori sono stati leggermente arrotondati.
Non vuol dire però che ciò non sia possibile raggiungere la potenza nominale, e che i 40 W siano solo ipotetici. Nella pratica, infatti, è possibile – sempre riflettendo sulla formula (2) – aumentare la potenza dissipabile a patto di aumentare anche la differenza Tj – Tamb; ad esempio ricorrendo ad un dissipatore raffreddato ad acqua, in modo da ridurre la “sua” Tamb di riferimento dai 25°C (in realtà all’interno dei contenitori si hanno dai 40 ai 60°C) fino ai 15°C o anche meno dell’acqua nelle condutture. Ciò significa poter dissipare anche il 25% della potenza in più.